6174 Constant de Kaprekar, un nombre curiós...

Un nombre màgic...

Sembla un número qualsevol, podria ser fins i tot un codi PIN, si sumem els seus dígits, dona 18 i ens queda clar que és un múltiple de 9.

Se'l coneix com a Constant de Kaprekar perquè és qui va descobrir la misteriosa bellesa de 6174 i la va presentar en la Conferència Matemàtica de Madràs en 1949.  Dattatreya Ramchandra Kaprekar (1905-1986), un addicte confés de la teoria dels números.

No confondre amb el Nombre de Kaprekar

"Un borracho quiere seguir bebiendo vino para permanecer en ese estado placentero. Lo mismo ocurre conmigo en lo que respecta a los números" (frase que se li atribueix en l'article de la BBC https://www.bbc.com/mundo/noticias-49426284.

En matemàtiques, la constant de Kaprekar és el resultat, sempre idèntic, d'aplicar iterativament la rutina de Kaprekar a un nombre natural de quatre xifres on com a mínim una és diferent. Aquest algorisme consisteix a reordenar els dígits del nombre de forma descendent i ascendent i obtenir la diferència entre els dos nombres obtinguts; al resultat se li torna a aplicar el mateix procediment, i així successivament. Per a nombres de quatre dígits (no iguals), el procés sempre condueix al número 6174 en menys de set iteracions.

 

Material: paper i llapis.

Procediment: Escriurem en un paper el número 6.174. El doblegarem i l'amagarem com a predicció.

Triarem una persona i li donarem les següents instruccions:

1. Pensa un número de quatre xifres, les que vulguis, com a mínim una ha de ser diferent.
2. Ordena les seves xifres de major a menor,
3. També les ordenes de menor a major.
4. D'aquests dos números, al major resta-li el petit.
5. Repeteix les passes 2, 3, 4 fins que el resultat no canviï.
6. No diguis el resultat ... perquè ja el tenim en el paper amagat.

 Solució: El resultat sempre és el número 6.174.

Per exemple, si prenem el número 2979:

Nombre Base	Ordenat ascendent	Ordenat descendent	Diferència
2979	9972	2799	7173
7173	7731	1377	6354
6354	6543	3456	3087
3087	8730	0378	8352
8352	8532	2358	6174
6174	7641	1467	6174

Quan arriba a 6174, el procés dona repetidament aquest mateix nombre, ja que ${\displaystyle 7641-1467=6174}$

No tot a la vida ha de ser útil, per ser atractiu, divertit i interessant, Kaprekar es va fer conegut dins i fora de l'Índia, i d'altres varen continuar jugant amb els números.

Yutaka Nishiyama, de la Universitat d'Economia d'Osaka, Japó, explica en la revista +plus, que va utilitzar un ordinador per veure si hi havia un nombre limitat de passes per arribar a 6174. Suposo que hi ha una estructura d'arbre tal com parla Kruskal amb la seva teoria, però avui se m'escapa de les mans. Qualsevol aportació serà benvinguda.

Podem concloure que el nombre màxim nombre de passes és 7, és a dir que si no arribes a 6174 després de fer l'algoritme de Kaprekar set cops, has fet un error de càlcul i cal revisar-ho.

També hi ha la versió amb tres xifres i veureu que sempre acabem amb 495.

Sembla que no passa amb cap altre nombre de xifres...

Ara proveu amb la vostra edat, l'any que vàreu néixer, el pin de la targeta, he, he, he.

6174 en tecnicolor

(Curiositat treta de:https://www.bbc.com/mundo/noticias-49426284)

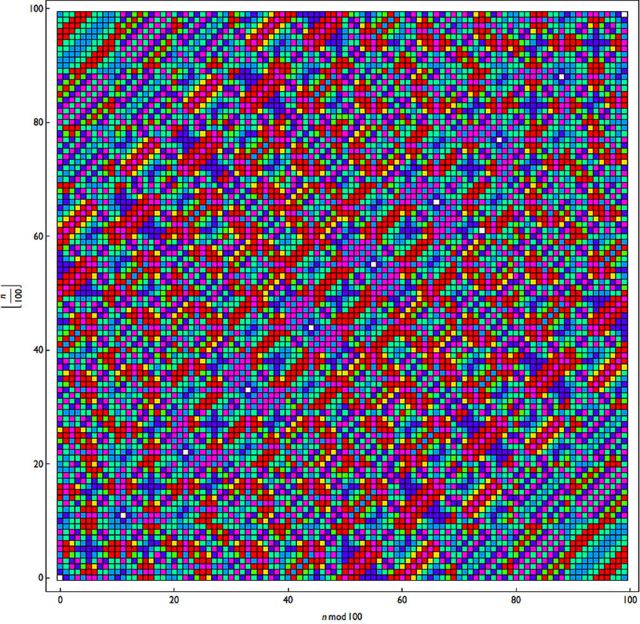
Entre tanto, en India, la empresa sin fines de lucro Scigram Technologies Foundation, que está desarrollando una "Plataforma de Aprendizaje Computacional" especialmente para las escuelas rurales y tribales, tomó el 6174 y lo convirtió en la colorida ilustración que verás abajo.

• Qué son los números imaginarios y por qué sin ellos no podrías leer esto

El cofundador Girish Arabale le explicó a BBC Mundo que lo que siempre buscan es inspirar especialmente a los niños de la escuela que generalmente odian las matemáticas, mostrándoles lo que llaman "momentos ¡Ajá!" para motivarlos.

La constante Kaprekar 6174 es uno de esos hermosos números y los pasos que conducen a su descubrimiento crean un momento '¡Ajá!' que generalmente falta en los currículos de matemáticas tradicionales".

Entonces, le asignaron un color a cada cantidad de pasos requeridos para llegar a 6174 (acuérdate que eran máximo 7 pasos):

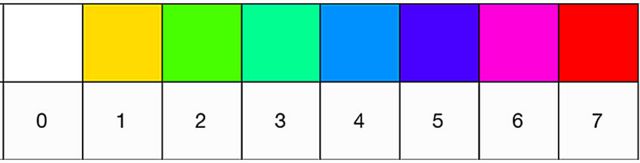
...escribieron un código que se puede recrear fácilmente en una Raspberry Pi (la computadora que es una herramienta popular en la educación STEM) en un idioma Wolfram, que está disponible gratuitamente en Raspberry Pi...... y ejecutaron el programa para cada uno de los 10.000 números de 4 dígitos que existen, creando patrones con los pasos que conducen al número 6174 dispuestos en una cuadrícula con los diferentes colores.

Més exemples 

Altres planes que he consultat:

 https://www.bbc.com/mundo/noticias-49426284

https://ca.wikipedia.org/wiki/Constant_de_Kaprekar  

https://ca.wikipedia.org/wiki/Nombre_de_Kaprekar

https://blogs.elespectador.com/actualidad/ecuaciones-de-opinion/6174-numero-fantastico

Estiu al Montessori, Matemàtica i Màgia, Repte 3 x 15

 https://www.estiualmontessori.com/project/repte-3x15-matematica-magia/

Aquest estiu la sort m'ha obert a porta a fer un taller al Montessori de matemàtiques i màgia.

Una gran sort afegida, he trobat la col·laboració incondicional d'en Jaume Andrés, i uns vailets supergenials, cosa que fa que ens ho passem la mar de bé tots plegats pencant d'allò més ...

Moltes gràcies, Susanna.

TALLER DE MATEMÀGIA

Col·legi Montessori - Palau Juliol 2022

Dins el programa Estiu al Montessori hi ha el Repte 3 x 15: Matemàtica i Màgia.

“T’agradaria deixar els teus amics i familiars bocabadats? En aquest projecte aprendràs a sorprendre i a sorprendre’t, ja que la màgia no només és font d’il·lusió sinó que també amaga principis matemàtics i científics que mai no t’hauries imaginat. Treu l’artista que portes dins, tot descobrint que les matemàtiques són màgiques.”

La màgia, per la seva càrrega lúdica, pel seu caràcter creatiu, de representació simbòlica i posada en escena, ofereix un meravellós camp de treball que l’utilitzarem com a recurs per introduir-hi la ciència i en concret la matemàtica. S'ha comprovat que la màgia constitueix un mitjà positiu per desenvolupar una sèrie d'habilitats relacionades amb la lògica i la creativitat, fomentant en l'alumne una millor predisposició a aprendre.

Objectius:

• Desplegar la creativitat, la imaginació i la innovació.

• Millorar la capacitat d’observació i atenció. Simplificar idees i redactar.

• Exercitar la memòria i el càlcul mental.

• Reforçar l’autoestima.

• Agafar seguretat en situacions imprevisibles.

• Treball en equip, millorar la relació amb els altres.

• Resolució de problemes

• Exercitar la crítica constructiva.

• Aprendre la manipulació i exploració d’objectes i idees

• Desplegar habilitats de comunicació, perdre la por a actuar en públic.

• Desenvolupar la faceta artística comprovant i creixent en les pròpies disposicions a l’art

• Aprendre “jocs de màgia” concrets, iniciant-se a l’ “il·lusionisme”.

• Despertar l’afició vers aquesta disciplina artística

Conceptes matemàtics aplicables a la màgia per a adolescents

• Principis de Simetria

• Principi d'Hummer

• Principi de paritat

• Principi del 9

• Principi de Kruskal

• Quadrats màgics

• Sistema de numeració Binari

• Piles de Gergonne i base 3

• Probabilitat

• Principi de Gilbreath

• Seqüència de Bruijn

Professors:

• Professor titular: Artur Antúnez (membre de la S.E.I. – A.C.A.I. Societat Espanyola d’Il·lusionisme) – Associació Catalana d’Il·lusionisme i de l’E.M.D.B. (Els Mags de Banyoles).

• Professor associat (voluntari) Jaume Andrés, membre de la S.E.I. – A.C.A.I.

Estructura del taller:

Primer dia:

• Presentació d’alumnes i profes

• Decàleg del mag i jurament

• Sondeig dels gustos, coneixements i nivell màgic dels alumnes (avaluació inicial)

• Primeres sorpreses

Cada dia:

• Repàs dels jocs del dia anterior (“un(a) que passi a fer-lo...”)

• Jocs nous del dia, amb la següent estructura:

  • presentació màgica del joc(s),

  • fonaments i base matemàtica de l'efecte,

  • tècnica i presentació (valorant l’originalitat de cadascú)

  • assaig per parelles – aprenentatge pel “sistema mutu”:

(“Tu li fas el joc a ell(a) i ell te’l fa a tu”)

• redacció personal de les instruccions. Enregistrament si s’escau

• A part del repàs, proposarem i invitarem els alumnes a presentar jocs que hagin après pel seu compte o versions dels jocs que hàgim après al taller.

Darrer dia:

• Assaig de l’espectacle

• Espectacle dels alumnes, amb invitats si ho desitgen

• Petita actuació dels professors

• Invitació a continuar conreant la màgia (informació d’associacions, escoles de màgia, botigues, recursos, webs...)

JOCS

Jocs Matemàtics:

(probablement, no arribarem a fer-los tots i possiblement els alumnes n’aportin d’altres)

• Amb números:

  • Saber el total sense saber els números

  • Endevinar el número ocult

  • Predicció del 1089

  • Els quadrats màgics (sumen el mateix en totes direccions)

• Amb fulls de calendari

  • Endevinar la suma de les dates de qualsevol “rectangle” de 3x3 o 4x4 dies

  • Endevinar la suma de quatre dies elegits secretament

• Amb daus

  • Endevinar la suma de les cares ocultes d’una torre de daus

  • Endevinar la posició de les 6 cares d’un dau estant d’esquena

  • Els punts canviants dels daus màgics

• Amb targetes

  • Els copets endevinadors

  • Test per a 5 parelles

  • The nine card problem (també es pot fer amb cartes)

  • On t’amagues? (la “casa encantada” de Copperfield)

  • Endevino el teu dibuix si em dius a quines targetes el veus

  • Endevinació personatges de Maths Star o Maths Potter (sistema binari)

• Amb llumins (també es poden fer amb monedes i altres objectes)

  • Endevinar si està cap per amunt o cap per avall

  • Sé quants en queden sense saber els que has posat

• Amb cartes

  • Les 21 cartes (endevinar una carta “pensada”)

  • Lladre i policia (automàtic bàsic)

  • La flor (o el cometa): Predicció d’una carta lliurement triada

  • El rellotge (t’endevino l’hora que has pensat i la carta sobre el nº de l’esfera)

  • Les cartes parlen al mag (el nº d’una carta endevina les que has mogut secretament)

  • Baralla Probabilística o test psicocromàtic (ordenació insòlita després de barrejar)

  • La balança humana (endevinar el nº de cartes pel seu “pes”)

  • Predicció sumant fins a 10

  • Endevinació de la “carta del dia”

• Amb altres objectes

  • On és la bola (estant amagada sota un de 3 gots opacs)

  • Un full escrit on per camins diferents tots arriben a la mateixa paraula

• Màgia topològica

  • La paradoxa dels trols, o la dels ous (puzle que movent fitxes desapareixen personatges)

  • El “vuit” de corda (que a les mans del mag es desfà i a les teves es fa un nus).

Altres jocs no-matemàtics adients a un taller d’iniciació a la màgia:

Sense cartes

Amb cartes

Gometes que salten d’un dit a l’altre L’anell trepador (puja gometa amunt) Corda que travessa el dit Corda i nusos Corda tallada i recomposta Els clips enamorats (s’enllacen sols) Els “palillos” (maneig de les paletes) El fil i la palleta (tallat i recompost) Sobres que fabriquen diners Llapis flexible (efecte òptic) Llapis que travessa un bitllet sense deixar forat Globus i Ampolla Globus i mòbil Globus dins d’un altre Globus que es pot punxar i continua inflat

Asos de Belchou Atracció de les cartes homòlogues Carta al cor (amb carta-guia a top) Intercanvi de reis a cegues La importància del 4t. piló “Mezcla del loco” (efecte de “triunfo”) Tu seràs el mag (sense saber-ho, faràs els moviments adients per trobar la meva carta) Endevinar una carta pensada (de les 10 primeres, fent pilonets) Assemblea d’ asos (la + senzilla Urzáiz)

Tècniques cartomàgiques elementals a practicar

• La carta-guia

• Transposició de top a bottom

• Falsa barreja Thurston

• Tallar en fals

• “pelar” cartes

• Posició “de donar” i “biddle”

• Primers intents de fer “l’extensió” i “el ventall”

• Ordenació Si Stebbins

 Material per al taller

Individual:

• Tapet per a cartes

• Dues Baralles (vermella i blava)

• 2 daus

• Material per a escriure (llapis i fulls)

• Corda (2 m.)

• 3 gots opacs d’un sol ús

De grup:

• Gomes elàstiques de mides i colors diferents

• Escuradents plans

• Clips

• Globus

• Fulls de “gomets”

• 2 capses de llumins de fusta ordinaris

Bibliografia

• Tamariz, Juan: “Por arte de Verbimagia”. Ed.: Frakson. Madrid 2005

• Gardner, Martin: “Magia Inteligente” Ed.: Granica. Buenos Aires 1988

• Roma, Josep et al.:“Manual de magia matemática con las cartas”. Ed. De Vecchi. BCN 1996

• Ruiz Xuxo: “Educando con magia”. Ed.: Narcea. Madrid 2013.

• Alegría Pedro: “Magia por principios”. Publidisa. Madrid 2008.

• González Francisco (Mago Paco): Matemagia. Autoedición. 2019

• Blasco Fernando:”Matemagia”. Ed.: Temas de hoy. 4ª edición. Madrid 2009

• “Profesor Raferty”: “Cómo orquestar un taller de magia”. Autoedición, 2ª ed. 2022

• Colombini Aldo: “Cartomagia improvisada”. Ed. Marré. Barcelona 2007.

• Canuto Vicente: “Cartomagia Fundamental”. Ed.: Icasa. 8ª edición. Sevilla 2008

• Luengo Jorge: “Super trucos mentales” Ed.: Planeta -Temas de hoy. Barcelona 2018.

III Encuentro de Magia, Ciencia y Educación.

III Encuentro de Magia, Ciencia y Educación.
Guadalajara, 1 - 3 d'abril de 2022.

Tinc la sort de tornar a participar en aquestes trobades, sempre és un repte el fet de posar ordre a allò que fas per poder-ho compartir. Així com trobar-nos amb gent de qui aprendre i compartir.

Aquest cop la intenció és que els participants s'animin a adaptar els models que utilitzo per crear jocs a  mida del que fas, sigui a l'aula o en la teva vida personal.

Tots recordem  mestres que han fet les classes més divertides. Ara ens toca intentar-ho nosaltres, si fem les classes, més divertides, captarem millor l’atenció del nostre alumnat, amb més motivació.

• La màgia del 9 i com emprar-la de diferents maneres per improvisar jocs aparentment diferents.
• Sistema de numeració en base 2 i tres, per endevinar noms, objectes ...
  Fer que cadascú dissenyi sobre qualsevol tema.
  
• També per portar un element a qualsevol posició desitjada.
• De Bruinj per fer quelcom senzill, però potent, per vestir-ho de mentalisme...
• Kruskal per fer servir en qualsevol text de qualsevol tema i llengua.

Començarem fent algun joc d'exemple de cada apartat, amb una presentació, amb l'objectiu de viure una emoció que és el que hem d'aprendre a transmetre. I veure diferents exemples per adaptar-lo cadascú al seu context o especialitat.

https://blogs.upm.es/magiayciencia/

https://www.escepticos.es/node/8515

https://magsci.eu/

https://exitoeducativo.net/el-iii-encuentro-de-ciencia-magia-y-educacion-promovera-el-pensamiento-critico-y-la-lucha-contra-la-pseudociencia/